Dado que las fuerzas están representadas por vectores, se pueden sumar de la misma manera que los vectores. Hay dos maneras de sumar fuerzas.
1 - Adición Geométrica de Fuerzas
El siguiente ejemplo muestra la adición de 3 fuerzas: F1, F2 y F3 a la izquierda. A la derecha están las mismas fuerzas desplazadas de manera que son paralelas a las fuerzas dadas y dispuestas de tal manera que el punto final de la primera fuerza (F1) coincide con el punto inicial de la segunda fuerza (F2); el punto final de la segunda fuerza coincide con el punto inicial de la tercera fuerza (F3). La suma R de las 3 fuerzas tiene el punto de inicio de la primera fuerza en la suma y el punto final de la última fuerza en la suma.
2 - Adición Analítica de Fuerzas Usando Componentes
Las fuerzas dadas por sus componentes se suman sumando sus componentes en x e y.
componentes.
Si por ejemplo F1 = ( F1x , F1y) y F2 = (F2x , F2y), entonces
F1 + F2 = (F1x + F2x , F1y + F2y)
Ejemplos con Soluciones Detalladas
Ejemplo 1
F1 y F2 son fuerzas dadas por sus magnitudes y direcciones en la figura de abajo. Encuentra la magnitud y la dirección de la fuerza R = F1 + F2. La dirección se define como el ángulo entre el eje x positivo y R.
Solución
Examinemos dos métodos.
Método 1: Geométrico / Trigonométrico; usando las leyes del coseno y seno
Usando la ley del coseno, podemos escribir
|R|2 = |F1 + F2|2 = |F1|2 + |F2|2 - 2 |F1| |F2| cos (25 + 44)
Usa |F1| = 20 y |F2| = 30, obtenemos
|R| = |F1 + F2| = √(202 + 302 - 2 (20)(30) cos (25 + 44)) ≈ 29.5 N
Usa la ley del seno para encontrar el ángulo α
sin(α) / 30 = sin (25 + 44) / 29.5
Resuelve para encontrar α ≈ 71.7°
La dirección de F1 + F2, definida como el ángulo entre F1 + F2 y el eje x positivo, es dada por
α + 25 ≈ 96.7°
Método 2: Analítico usando componentes
Expresa F1 y F2 usando componentes
F1 = (20 cos 25° , 20 sin 25°) y F2 = (-30 cos 44° , 30 sin 44°)
F1 + F2 = (20 cos 25° , 20 sin 25°) + (-30 cos 44° , 30 sin 44°) = (20 cos 25° - 30 cos 44° , 20 sin 25° + 30 sin 44°) ≈ (-3.5 , 29.3)
|F1 + F2| = √ ( (-3.5)2 + 29.32) ≈ 29.5 N
Dirección: Si el punto inicial de F1 + F2 está en el origen, el punto terminal de F1 + F2 está en el cuadrante II, por lo tanto el ángulo entre el eje x positivo y F1 + F2 es dado por
180° - |arctan (29.3 / - 3.5)| ≈ 96.8°
El segundo método es más eficiente (toma menos tiempo) que el primer método cuando el número de fuerzas a sumar es mayor de 3.
Un video con más ejemplos en Resultante de Dos Fuerzas
Ejemplo 2
¿Cuál es la magnitud y la dirección de F3 en el sistema de tres fuerzas a continuación para que F1 + F2 + F3 = 0?
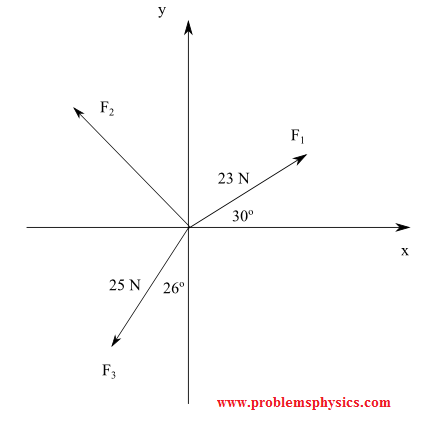
Solución
Expresa F1, F2 y F3 por sus componentes
F1 = (23 cos 30° , 23 sin 30°)
F2 = (|F2| cos θ , |F2| sin θ) , donde θ es el ángulo entre el eje x positivo y F2
F1 = (-25 sin 26° , - 25 cos 26°)
(23 cos 30° , 23 sin 30°) + (|F2| cos θ , |F2| sin θ) + (- 25 sin 26° , - 25 cos 26°) = 0
23 cos 30° + |F2| cos θ - 25 sin 26° = 0
23 sin 30° + |F2| sin θ - 25 cos 26° = 0
Las ecuaciones anteriores dan
|F2| cos θ = 25 sin 26° - 23 cos 30° ≈ -9.0
|F2| sin θ = 25 cos 26° - 23 sin 30° ≈ 10.1
|F2|2 = (25 sin 26° - 23 cos 30°)2 + (25 cos 26° - 23 sin 30°)2
|F2|2 ≈ 13.9 N
θ = 180 - arctan(10.1 / 9.0) ≈ 131.7°
Ejemplo 3
¿Cuál es la relación entre las magnitudes |W| y |N| de las fuerzas W y N, con W dirigida en la dirección del eje y negativo y N en la dirección del eje y positivo y tal que W + N = 0?
Solución
Primero expresamos W y N por sus componentes de la siguiente manera
W = (0 , -|W|) y N = (0 , |N|)
W + N = (0 , -|W|) + (0 , |N|) = 0
Usando los componentes en y, obtenemos
-|W| + |N| = 0
|W| = |N|
Más Referencias y Enlaces