Componentes de una Fuerza en un Sistema de Coordenadas
Componentes de una Fuerza
Siendo un vector
, una fuerza
se puede representar mediante sus componentes, como cualquier vector. Una de las principales ventajas de descomponer las fuerzas en sus componentes es que resulta fácil sumarlas, multiplicarlas por un escalar, etc.
Si |F| es la magnitud y θ es el ángulo entre la dirección positiva del eje x y la fuerza F, entonces los componentes Fx y Fy están dados por
Fx = |F| cosθ y Fy = |F| sinθ
Por lo tanto, F puede escribirse en términos de sus componentes de la siguiente manera:
F = (Fx , Fy) = (|F| cosθ , |F| sinθ)
Un video con más ejemplos sobre Componentes de Vectores
y otro video con más ejemplos sobre Componentes de Fuerzas están incluidos.
Ejemplos con Soluciones Detalladas
Ejemplo 1
Encuentra los componentes de una fuerza F cuya magnitud es de 20 N y cuya dirección está definida por un ángulo θ = 30° formado por la fuerza y el eje x positivo, como se muestra a continuación.
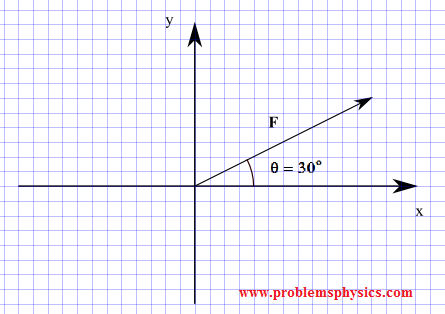
Solución
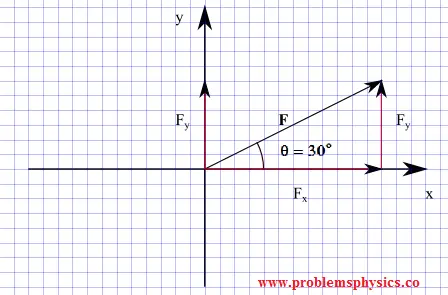
Sean los componentes de la fuerza (vector) F Fx y Fy, como se muestra en el diagrama a continuación.
Usando el triángulo rectángulo formado por F, Fx y Fy, podemos escribir:
sin θ = Fy / |F|
cos θ = Fx / |F|
donde |F| es la magnitud de la fuerza F.
Lo anterior puede escribirse como
Fx = |F| cos θ = 20 cos 30° = 10 √3
Fy = |F| sin θ = 20 sin 30° = 10
F = (10 √3 , 10)
Ejemplo 2
Encuentra los componentes de una fuerza cuya magnitud es de 50 N y cuya dirección está definida por un ángulo α = 25° formado con el eje y negativo, como se muestra en el diagrama a continuación.
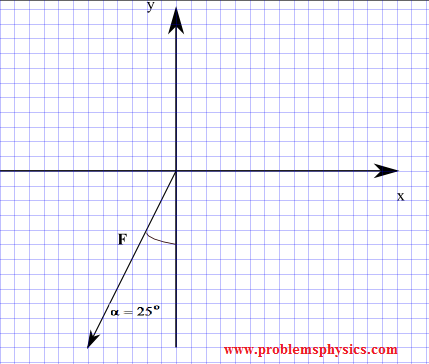 _
_
Solución

Sean Fx y Fy los componentes de F como se muestra en el diagrama a continuación.
Usando el triángulo rectángulo formado por F, Fx y Fy, escribimos:
sin α = - Fx / |F|
cos α = - Fy / |F|
El signo negativo en - Fx / |F| y - Fy / |F| toma en cuenta el hecho de que Fx y Fy son negativos. Por lo tanto:
Fx = - |F| sin α = - 50 sin 25° ≈ - 21.1
Fy = - |F| cos α = - 50 cos 25° ≈ - 45.3
F = (- 21.1 , - 45.3)
Ejemplo 3
En el diagrama a continuación, la fuerza F es paralela a la pierna CB del triángulo rectángulo ABC.
a) Determina los componentes de la fuerza F en términos de la magnitud de F y del ángulo α. El sistema de coordenadas x-y tiene el eje x paralelo a AC y el eje y perpendicular a AC, como se muestra en el diagrama.
b) Encuentra los valores numéricos de los componentes para |F| = 100 N y α = 30°.
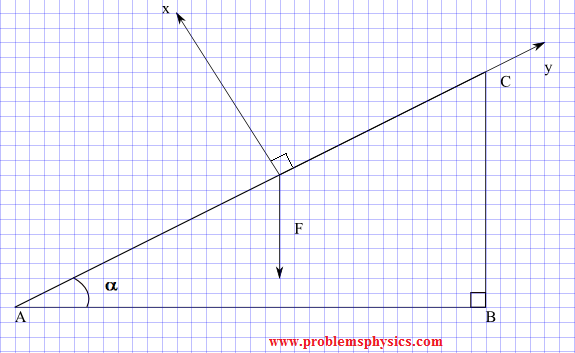
Solución
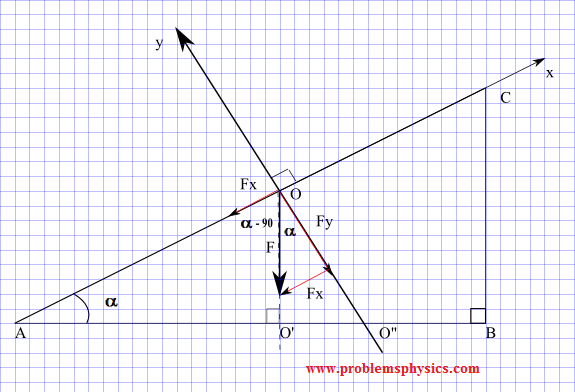
El triángulo rectángulo AOO' tiene los ángulos α, 90°-α y 90°.
Dado que AC es perpendicular a OO", el ángulo AOO' es igual a 90° y, por lo tanto, el ángulo O'OO" es igual a α
Consideremos el triángulo rectángulo formado por F, Fy y Fx.
sin α = - Fx / |F| (el signo negativo se debe a que Fx es negativo)
cos α = - Fy / |F| (el signo negativo se debe a que Fy es negativo)
lo cual nos da:
Fx = - |F| sin α
Fy = - |F| cos α
F = (- |F| sin α , - |F| cos α)
|F| = 100 , α = 30°
Fx = - |F| sin α = -100 sin 30° = - 50
Fy = - |F| cos α = -100 cos 30° = - 50 √ 3
F = (-50 , - 50 √ 3)
Nota: El ejemplo anterior es muy útil en problemas relacionados con fuerzas en planos inclinados.
Ejemplo 4
Tres fuerzas F1, F2 y F3 de magnitudes 80 N, 60 N y 50 N en el mismo sistema de ejes, tales que F1 está dirigida a lo largo del eje x positivo; F2 en la dirección dada por el rumbo N25E y F3 a lo largo del eje y negativo.
Encuentra los componentes de cada fuerza.
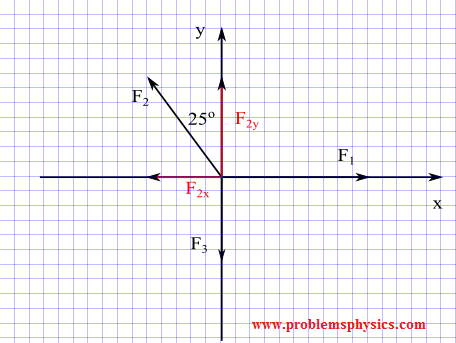
Solución
Primero construimos un diagrama usando las direcciones dadas anteriormente.
F1 está dirigida a lo largo del eje x, por lo tanto, un componente a lo largo del eje x es igual a |F| y el componente a lo largo del eje y es igual a 0.
F1 = (|F1| , 0) = (80 , 0)
F2 está dirigida a lo largo del eje y negativo, por lo tanto:
F2 = (0 , -|F2|) = (0 , - 60)
F3 es tal que el componente x es negativo y el componente y es positivo; usando el triángulo rectángulo formado por F2, F2x y F2y, escribimos:
F3 = (F2x , F2y) = (-60 sin 25° , 60 cos 25°)
Ejemplo 5
Expresa cada una de las fuerzas A, B, C y D mostradas en la figura a continuación mediante sus componentes.
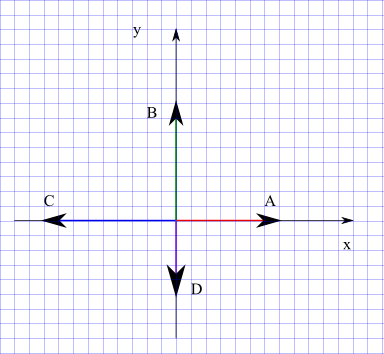
Solución
Cada una de las cuatro fuerzas está dirigida ya sea a lo largo del eje x o del eje y en la dirección negativa o positiva.
A = (|A| cos 0° , |A| sin 0°) = ( |A| , 0)
B = (|B| cos 90° , |B| sin 90°) = (0 , |B|)
C = (|C| cos 180° , |C| sin 180°) = (-|B| , 0)
D = (|D| cos 270° , |D| sin 270°) = (0 , -|C|)


 _
_




