Se presenta una calculadora en línea de fuerza resultante .
Fuerza Resultante
La fuerza resultante debida a varias fuerzas \( \vec {F}_1, \vec {F}_2, ... \) que actúan sobre un objeto es la fuerza \( \vec {R}f \) que tiene los mismos efectos físicos que las diferentes fuerzas que actúan sobre ese objeto.
Matemáticamente, la fuerza resultante \( \vec {R}f \) se da por la suma vectorial de todas las fuerzas que actúan sobre el objeto.
\[ \vec {R}f = \vec {F}_1 + \vec {F}_2 + .... \]
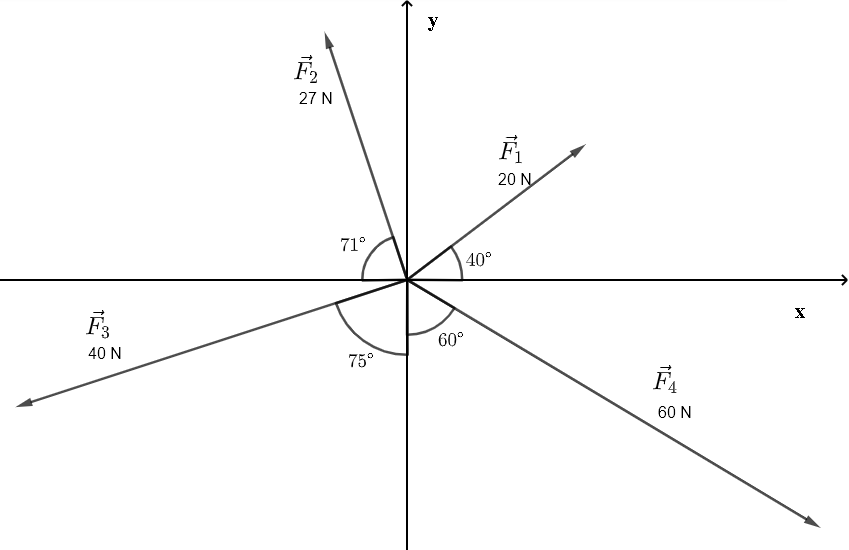
Dada la magnitud y la dirección de cada fuerza, la calculadora presentada a continuación calcula los componentes de cada fuerza dada, luego suma los componentes \( x \) de las fuerzas \( \vec {F}_1, \vec {F}_2, ... \) para obtener el componente \( R_{fx} \) y luego suma los componentes \( y \) de las fuerzas \( \vec {F}_1, \vec {F}_2, ... \) para obtener los componentes \( R_{fy} \).
La magnitud \( |\vec {R}f| \) y la dirección \( \theta \) de la fuerza resultante \( \vec {R}f \) se dan por
\[ |\vec {R}f| = \sqrt { ( R_{fx} )^2 + ( R_{fy} )^2} \]
\[ \theta = \tan^{-1} \left({\frac{R_{fy}}{R_{fx}}}\right) \] con \( \theta \) en el rango \( [0 , 2\pi) \) teniendo en cuenta el cuadrante donde están los componentes de la resultante \( \vec {R}f \).
Uso de la Calculadora de Fuerza Resultante
1 - Ingrese la magnitud \( |F_i| \) y la dirección de cada fuerza.
Importante
A) La dirección es el ángulo medido desde el lado positivo del eje x y está en grados.
B) Las magnitudes y direcciones de las cuatro fuerzas \( \vec {F}_1, \vec {F}_2, \vec {F}_3, \vec {F}_4, \) en el diagrama anterior se utilizan como valores predeterminados cuando inicia esta página. Las direcciones dadas por diferentes ángulos se han convertido en ángulos desde el eje x positivo hasta la fuerza representada por un vector en el diagrama anterior.
2 - Haga clic en "Calcular" para obtener \( R_{fx} \) y \( R_{fy} \), que son los componentes x e y de la resultante \( \vec {R}f \), su magnitud y su dirección \( \theta \) definida anteriormente.