Resistencias en Serie y Paralelo
Presentamos ejemplos de circuitos con resistencias en serie y paralelo y las fórmulas para calcular la resistencia equivalente de estos grupos de resistencias.
Resistencias en Serie
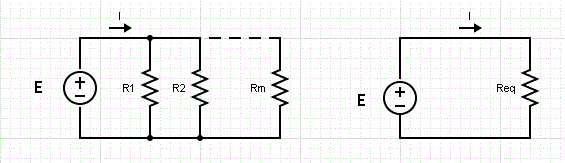
Las resistencias R1, R2 ..., Rm en el circuito del lado izquierdo se dicen que están en serie porque la misma corriente pasa a través de ellas. Se comportan de la misma manera que el circuito de la derecha con una resistencia Req dada por la suma de las resistencias R1, R2 y R3.
Req = R1 + R2 ....+ Rm
La corriente I en el circuito anterior se da por:
I = E / Req
Resistencias en Paralelo
El voltaje a través de cada una de las resistencias R1, R2 ..., Rm en el circuito de la izquierda es el mismo y, por lo tanto, estas resistencias se dicen que están en paralelo. Se comportan de la misma manera que el circuito de la derecha con una resistencia Req que se da por la ecuación:
1 / Req = 1 / R1 + 1 / R2 + .... + 1 / Rm
Resistencias en Serie: Ejemplos con Soluciones Detalladas
Ejemplo 1
Encuentra la corriente I que pasa a través de las resistencias y el voltaje en cada una de ellas en el siguiente circuito.
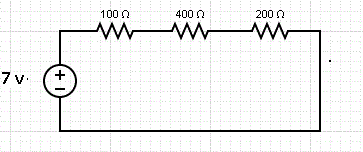
Las tres resistencias en serie tienen una resistencia Req dada por la suma de las tres resistencias. Por lo tanto:
Req = 100 + 400 + 200 = 700 Ω
La corriente I que pasa por R1, R2 y R3 es la misma y se calcula de la siguiente manera:
I = 7 V / 700 Ω = 0.01 A
El voltaje a través de cada resistencia se calcula usando la ley de Ohm de la siguiente manera:
El voltaje a través de 100Ω: VR1 = 100 × I = 100 × 0.01 = 1 V
El voltaje a través de 400Ω: VR2 = 400 × I = 400 × 0.01 = 4 V
El voltaje a través de 200Ω: VR3 = 200 × I = 200 × 0.01 = 2 V
Resistencias en Paralelo: Ejemplos con Soluciones Detalladas
Ejemplo 2
Encuentra la corriente I en el circuito de abajo y la corriente que pasa a través de cada una de las resistencias en el circuito.
Solución al Ejemplo 2
Las tres resistencias están en paralelo y se comportan como una resistencia con una Req dada por:
1 / Req = 1 / 100 + 1 / 400 + 1 / 200
Multiplica todos los términos por 400 y simplifica para obtener:
400 / Req = 4 + 1 + 2
Resuelve para obtener:
Req = 400 / 7 Ω
La corriente principal I está dada por:
I = 7 / Req = 7 / (400 / 7) = 49 / 400 A
Ahora usamos la ley de Ohm para encontrar la corriente que pasa por cada resistencia.
La corriente a través de la resistencia de 100 Ω: I1 = 7 / 100 A
La corriente a través de la resistencia de 400 Ω: I2 = 7 / 400 A
La corriente a través de la resistencia de 200 Ω: I3 = 7 / 200 A
Como ejercicio, verifica que la suma de las tres corrientes anteriores es igual a la corriente I = 49 / 400 A.
Resistencias en Serie y Paralelo: Ejemplos con Soluciones Detalladas
Ejemplo 3
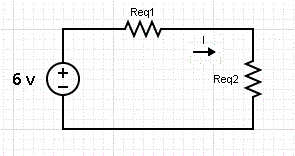
Encuentra la corriente I en el siguiente circuito.
Solución al Ejemplo 3
Las dos resistencias en serie se agrupan como Req1 en el circuito equivalente a continuación, y su resistencia está dada por la suma:
Req1 = 100 + 400 = 500 Ω
Las dos resistencias en paralelo se agrupan como Req2 en el circuito equivalente a continuación y su resistencia está dada por la ecuación:
1 / Req2 = 1 / 100 + 1 / 200
Resuelve para obtener:
Req2 = 200 / 3 Ω
Req1 y Req2 están en serie y, por lo tanto, son equivalentes a una R dada por la suma:
R = Req1 + Req2 = 500 + 200 / 3 = 1700 / 3 Ω
Ahora usamos la ley de Ohm para encontrar la corriente I.
I = 6 / R = 6 / (1700 / 3) = 18 / 1700 A
Ejemplo 4
¿Qué resistencia x en paralelo con resistencias de 100 Ω y 200 Ω da una resistencia equivalente de 50 Ω?
Solución al Ejemplo 4
Sea x la resistencia a encontrar. La resistencia equivalente de las tres resistencias en paralelo es conocida. Usamos la ecuación que da la resistencia equivalente de resistencias en paralelo de la siguiente manera:
1 / 50 = 1 / 100 + 1 / 200 + 1 / x
lo que nos da:
1 / x = 1 / 50 - 1 / 100 - 1 / 200
Coloca todas las fracciones a la derecha con un denominador común de 200 y reescribe la ecuación de la siguiente manera:
1 / x = 4 / 200 - 2 / 200 - 1 / 200 = 1 / 200
Resuelve para x y obtén:
x = 200 Ω
Ejemplo 5
Demuestra que si las resistencias con resistencias R1, R2 ,..., Rm están en paralelo, entonces la resistencia equivalente Req siempre es menor que R1, R2, ..., Rm.
Solución al Ejemplo 5
La resistencia equivalente Req está dada por la ecuación:
1 / Req = 1 / R1 + 1 / R2 + ... + 1 / Rm
Dado que R1, R2, ... Rm son cantidades positivas, podemos escribir que:
1 / Req > 1 / Ri, donde Ri es cualquiera de las resistencias.
Multiplica todos los términos de la desigualdad anterior por (Req × Ri) y simplifica para obtener:
Ri > Req
o
Req < Ri, i = 1, 2, ... m.
Más Referencias y Enlaces
Ley de Ohm con Ejemplos
Soluciones de Prueba SAT II de Física sobre Circuitos Eléctricos DC