An optical fiber consists of a core with refractive index \(n_1\) and cladding with refractive index \(n_2\), where \(n_1 > n_2\). For total internal reflection at the core-cladding interface, the angle of incidence \(\theta\) must exceed the critical angle \(\theta_c\) given by:
\[ \theta_c = \sin^{-1}\left(\frac{n_2}{n_1}\right) \]
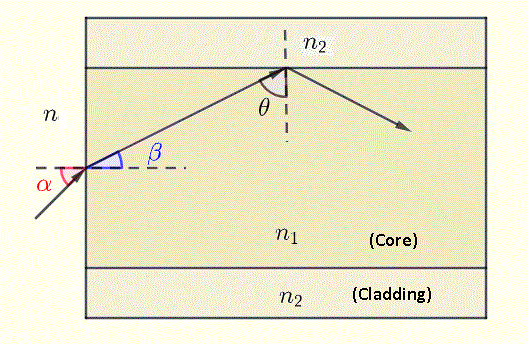
When light enters from a medium of refractive index \(n\) at angle \(\alpha\), it refracts to angle \(\beta\) inside the core. By Snell's law:
\[ n \sin\alpha = n_1 \sin\beta \]
Since \(\theta\) and \(\beta\) are complementary (\(\theta + \beta = 90^\circ\)):
\[ \cos\theta = \sin\beta \]
Thus:
\[ n \sin\alpha = n_1 \cos\theta \quad\Rightarrow\quad \theta = \cos^{-1}\left(\frac{n \sin\alpha}{n_1}\right) \]
For total internal reflection, \(\theta > \theta_c\):
\[ \cos^{-1}\left(\frac{n \sin\alpha}{n_1}\right) > \sin^{-1}\left(\frac{n_2}{n_1}\right) \]
Taking cosine of both sides (noting \(\cos x\) is decreasing on \([0, \pi/2]\)):
\[ \frac{n \sin\alpha}{n_1} < \sqrt{1 - \frac{n_2^2}{n_1^2}} \]
Simplifying:
\[ \sin\alpha < \frac{1}{n}\sqrt{n_1^2 - n_2^2} \]
The numerical aperture (NA) is defined as:
\[ \boxed{NA = \sqrt{n_1^2 - n_2^2}} \]
And the acceptance angle \(\alpha_{\text{max}}\) is:
\[ \boxed{\alpha_{\text{max}} = \sin^{-1}\left(\frac{NA}{n}\right)} \]
Light incident within \(\alpha_{\text{max}}\) undergoes total internal reflection and propagates through the fiber.
Use our numerical aperture calculator to verify solutions.
Given \(n = 1\), \(n_1 = 1.46\), \(n_2 = 1.45\):
a) Find the critical angle \(\theta_c\) at the core-cladding interface.
b) Calculate the numerical aperture \(NA\).
c) Determine the acceptance angle \(\alpha_{\text{max}}\).
Solution:
a) \(\theta_c = \sin^{-1}\left(\dfrac{n_2}{n_1}\right) = \sin^{-1}\left(\dfrac{1.45}{1.46}\right) \approx 83.29^\circ\)
b) \(NA = \sqrt{n_1^2 - n_2^2} = \sqrt{1.46^2 - 1.45^2} \approx 0.17\)
c) \(\alpha_{\text{max}} = \sin^{-1}(NA) \approx \sin^{-1}(0.17) \approx 9.82^\circ\)
Using the same values as Problem 1, with \(\alpha = 5^\circ\) at the air-core interface:
a) Find the refraction angle \(\beta\).
b) Calculate \(\theta\).
c) Explain why the ray is guided.
Solution:
a) Snell's law: \(n\sin\alpha = n_1\sin\beta \Rightarrow \beta = \sin^{-1}\left(\dfrac{\sin 5^\circ}{1.46}\right) \approx 3.42^\circ\)
b) \(\theta = 90^\circ - \beta \approx 86.58^\circ\)
c) Since \(\theta \approx 86.58^\circ > \theta_c \approx 83.29^\circ\), total internal reflection occurs. Equivalently, \(\alpha = 5^\circ < \alpha_{\text{max}} \approx 9.82^\circ\).
Given \(n = 1\), \(n_1 = 1.48\), find \(n_2\) such that rays with \(\alpha > 12^\circ\) are not guided.
Solution:
Set \(\alpha_{\text{max}} = 12^\circ\):
\[
\sin\alpha_{\text{max}} = \sqrt{n_1^2 - n_2^2} \Rightarrow n_2 = \sqrt{n_1^2 - \sin^2\alpha_{\text{max}}}
\]
\[
n_2 = \sqrt{1.48^2 - \sin^2 12^\circ} \approx 1.465
\]
Given \(n = 1\), \(\alpha_{\text{max}} = 10^\circ\), and \(\theta_c = 82^\circ\), find \(n_1\) and \(n_2\).
Solution:
From definitions:
\[
\sin\alpha_{\text{max}} = \sqrt{n_1^2 - n_2^2} \quad\text{and}\quad \sin\theta_c = \frac{n_2}{n_1}
\]
Solving:
\[
n_1 = \frac{\sin\alpha_{\text{max}}}{\cos\theta_c} = \frac{\sin 10^\circ}{\cos 82^\circ} \approx 1.248
\]
\[
n_2 = n_1 \sin\theta_c \approx 1.248 \times \sin 82^\circ \approx 1.236
\]
Optical Fibers
Numerical Aperture Calculator
Total Internal Reflection
Refraction of Light