Inclined Planes Problems with Solutions

Introduction

Inclined plane problems involving gravity, forces of friction , moving objects etc. require vector representations of these quantities. Components are better in representing forces using rectangular system of axes since they make calculations such as the addition of forces easier. Free body diagrams are also used as well as Newton's second law to write vector equations.

A video with examples on Components of Vectors may be helpful.

Problems with Detailed Solutions

Problem 1 (No friction)

A 2 Kg box is put on the surface of an inclined plane at 27 ° with the horizontal. The surface of the inclined plane is assumed to be frictionless.
a) Draw a free body diagram of the box on the inclined plane and label all forces acting on the box.
b) Determine the acceleration a of the box down the plane.
c) Determine the magnitude of the force exerted by the inclined plane on the box.

Solution
a)
Free Body Diagram
box on a frictionless inclined plane
Let the small blue point be the box
Two forces act on the box: the weight W of the box and N the force normal to and exerted by the inclined plane on the box (blue point)
b)
Use system of axes x-y as shown to write all forces in their components form

forces on a box in a frictionless inclined plane

Vectors N, W and a in components form:
     N = (0 , |N|)
     W = (Wx , Wy) = (|W| cos (27°) , - |W| sin (27°))
     a = (a_x , a_y) = (|a| , 0) , box moving down the inclined plane in the direction of positive x hence a_y = 0.
Use Newton's second law to write that the sum of all forces on the box is equal to the mass times the acceleration (vector equation)
     W + N = M a , M is the mass of the box
In components form, the above equation becomes
     (|W| sin (27°) , - |W| cos (27°)) + (0 , |N|) = M (|a| , 0)
For two vectors to be equal, their components must be equal. Hence
     x-components are equal : |W| sin (27°) + 0 = M |a|
     y-components are equal : - |W| cos (27°) + |N|= 0
     M |a| = |W| sin (27°)
weight: |W| = M g ; g = 10 m/²
|a| = M g sin (27°) / M = g sin (27) m/s^2 ≈ 4.5 m/s^2
c)
|N| = |W| cos (27°) = 2 × 10 cos (27°) ≈ 17.8 N

Problem 2

A particle of mass 5 Kg rests on a 30° inclined plane with the horizontal. A force F_a of magnitude 30 N acts on the particle in the direction parallel and up the inclined plane.
a) Draw a Free Body Diagram including the particle, the inclined plane and all forces acting on the particle with their labels.
b) Find the force of friction acting on the particle.
c) Find the normal force exerted by the inclined on the particle.

Solution
a)

Free Body Diagram
The box is the small blue point. In the diagram below, W is the weight of the box, N the normal force exerted by the inclined plane on the box, F_a is the force applied to have the box in equilibrium and F_s the force of friction opposite F_a.
box on an inclined plane with friction
b)

forces with components inclined plane with friction

The box is at rest, hence its acceleration is equal to 0, therefore the sum of all forces acting on the box is equal to its mass times its acceleration which is zero. ( Newton's second law)
     F_a + W + N + F_s = 0
The components form of all forces (vectors) acting on the box are:
     F_a = (30 , 0)
     |W| = 5 × 10 = 50 N
     W = (W_x , W_y) = ( - |W| sin(30°) , - |W| cos(30°)) = (- 50 sin (30°) , - 50 cos (30°) )
     N = (0 , |N|)
     F_s = (-|F| , 0)
The F_a + W + N + F_s = 0 in components form:
     (30 , 0) + (- 50 sin (30°) , - 50 cos (30°) ) + (0 , |N|) + (-|F| , 0) = 0
     x components: 30 - 50 sin(30) + 0 - |F| = 0
     |F| = - 50 sin(30) + 30 = 5 N
c)
y components equation:
     0 - 50 cos (30) + |N| + 0 = 0
     |N| = 50 cos (30) = 25 √3 ≈ 43.3 N

Problem 3

A box of mass M = 10 Kg rests on a 35° inclined plane with the horizontal. A string is used to keep the box in equilibrium. The string makes an angle of 25 ° with the inclined plane. The coefficient of friction between the box and the inclined plane is 0.3.

box held with string on inclined plane with friction

a) Draw a Free Body Diagram including all forces acting on the particle with their labels.
b) Find the magnitude of the tension T in the string.
c) Find the magnitude of the force of friction acting on the particle.

Solution
a)

Free Body Diagram
T tension of string, W weight of the box, N force normal to and exerted by the inclined plane on the box, F_s is the force of friction

b)
Forces and their components on the x-y system of axis.
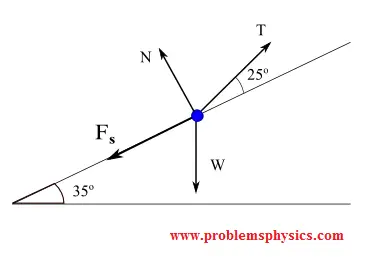
components of forces on inclined plane box with string

Equilibrium: W + T + N + F_s = 0
Forces represented by their components
     W = (Wx , Wy) = ( - M g sin(35°) , - M g cos(35°))
     T = (Tx , Ty) = (|T| cos (25°) , |T| sin (25°) )
     N = (0 , Ny) = (0 , |N|)
F_s = (- |F_s| , 0) = ( - μ_s |N| , 0) , where μ_s is the coefficient of friction between the box and the inclined plane.
Sum of x components = 0
- M g sin(35°) + |T| cos (25°) + 0 - μ_s |N| = 0
which may be rewritten as
     |T| cos (25°) = μ_s |N| + M g sin(35°)
sum of y components = 0
     - M g cos(35°) + |T| sin (25°) + |N| + 0 = 0
     |T| sin (25°) = M g cos(35°) - |N|
We now need to solve the system of two equations with two unknowns |T| and |N|.
     |T| cos (25°) = μ_s |N| + M g sin(35°) (equation 1)
     |T| sin (25°) = M g cos(35°) - |N| (equation 2)
solve equation 2 above for |N| to get
     |N| = M g cos(35°) - |T| sin (25°)
Substitute |N| by M g cos(35°) - |T| sin (25°) in eq 1 to get
     |T| cos (25°) = μ_s [ M g cos(35°) - |T| sin (25°) ] + M g sin(35°)
rewrite above equation as follows
     |T| [ cos (25°) + μ_s sin (25°) ] = μ_s M g cos(35°) + M g sin(35°)
Solve for |T|

|T| =

μ_s M g cos(35°) + M g sin(35°)

cos (25°) + μ_s sin (25°)

Substitute with numerical Values
μ_s = 0.3, M = 10 Kg, g = 10 m/s^2
|T| ≈ 79.3 N
c)
Use |N| = M g cos(35°) - |T| sin (25°) found above
|N| = 100 cos(35°) - 79.3 sin (25°) ≈ 48.4 N

Problem 4

A 100 Kg box is to be lowered at constant speed down an inclined plane 4 meters long from the back of a lorry 2 meters above the ground. The coefficient of kinetic friction is equal to 0.45. What is the magnitude of the force Fa to be applied parallel to the inclined plane to hold back the box so that it is lowered at constant speed?

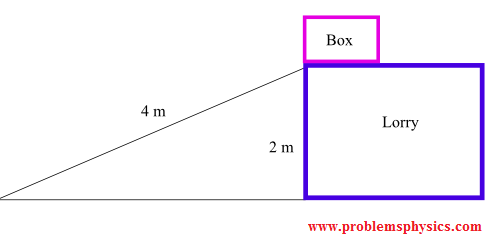
Solution

Free Body Diagram
forces acting on the box (purple point) and their components.
W weight of the box, N the normal force exerted by the inclined plane on the box, F_a the applied force so that the box is lowered at constant speed and F_k kinetic force of friction (box is moving downward, force of friction opposite motion).

forces acting on box from loory down an inclined plane

Components of all forces
     N = (0 , Ny) = (0 , |N|)
     F_a = (|F_a| , 0)
     F_k = (|F_k| , 0)
     W = (- M g sin α , - M g cos α )
Second Newton's law: constant speed means acceleration = 0, sum of all forces equals mass times acceleration, hence
     W + N + F_a + F_k = 0 (vector form)
component equations
     x components: 0 + |F_a| + |F_k| - M g sin α = 0 (eq 1)
     y components: |N|+0 + 0 - M g cos α = 0 (eq 2)
equation (2) gives
     |N| = M g cos α
kinetic force of friction formula: |Fk| = μ_k |N| = μ_k M g cos α
substitute |Fk| by μ_k M g cos α into equation (1)
     |Fa| = M g sin α - |Fk| = M g sin α - μ_k M g cos α
M = 100 Kg, g = 10 m/s^2
sin α = 2/4 = 1/2
sin α = √(1 - sin² α) = √3 / 2
     |Fa| = 1000 (1/2 - 0.45 √3 / 2) ≈ 110.3 N

Problem 5

A box of mass M = 7 Kg is held at rest on a 25° inclined plane by force Fa acting horizontally as shown in the figure below. The box is on the point of sliding down the inclined plane. The static coefficient of friction between the box and the inclined plane is μ_s = 0.3. Find the magnitude of force F_a.

forces acting horizontally on box down in an inclined plane

Solution
Free Body Diagram
components of forces acting on box on an inclined plane

     W = (-M g sin α , -M g cos α )
     N = (0 , |N|)
     F_a = (|F_a| cos α , - |F_a| sin α)
     F_s = (|F_s| , 0) = (μ_s|N| , 0)
sum of all x components = 0 gives:
     - M g sin α + 0 + |F_a| cos α + μ_s|N| = 0 (equation 1)
sum of all ycomponents = 0 gives:
     - M g cos α + |N| - |F_a| sin α + 0 = 0 (equation 2)
Equation (2) gives:
     |N| = |F_a| sin α + M g cos α
Substitute |N| by |F_a| sin α + M g cos α in equation (1) to get
     - M g sin α + |F_a| cos α + μ_s( |F_a| sin α + M g cos α ) = 0
     |F_a| (cos α + μ_s sin α ) = M g sin α - μ_s M g cos α

|F_a| =

M g sin α - μ_s M g cos α

cos α + μ_s sin α

Numaerical values
M = 7 Kg, α = 25°, μ_s = 0.3
|F_a| = 70 [ sin 25° - 0.3 cos 25° ] / [ cos 25° + 0.3 sin 25° ] ≈ 10.2 N