SAT Physics: Electromagnetism Practice Questions with Detailed Solutions

This resource provides comprehensive solutions to SAT Physics electromagnetism questions. Each solution includes detailed explanations, relevant formulas in LaTeX notation, and key concepts. Use these problems to strengthen your understanding of electromagnetic principles for the SAT Physics Subject Test.

Electromagnetism Concepts Covered

Transformers and electromagnetic induction
Motional electromotive force (EMF)
Faraday's Law of electromagnetic induction
Lenz's Law and direction of induced current
Magnetic flux and its calculation
Electric motors and energy transformation

Question 1: Transformer with AC and DC Components

The primary of a transformer is connected to a voltage source with two components: an alternating current (AC) component of 120 V and a steady direct current (DC) component of 5 V. The primary has 300 turns and the secondary has 6000 turns. What is the voltage at the output of the secondary?

A) 2400 V AC and 100 V DC

B) 2400 V AC only

C) 100 V DC only

D) 2500 V AC only

E) 2500 V DC only

Solution – Explanation

Transformers only work with alternating current (AC). A changing magnetic field in the primary coil induces a voltage in the secondary coil. Steady DC current produces a constant magnetic field that doesn't change with time, so it cannot induce a voltage in the secondary coil.

The transformer equation relates the voltages and number of turns:

\[ \frac{V_s}{V_p} = \frac{N_s}{N_p} \]

Where:

\(V_s\) = secondary voltage
\(V_p\) = primary voltage (AC component only, since DC is blocked)
\(N_s\) = number of turns in secondary coil = 6000
\(N_p\) = number of turns in primary coil = 300

Substituting the values:

\[ \frac{V_s}{120\ \text{V}} = \frac{6000}{300} = 20 \] \[ V_s = 120 \times 20 = 2400\ \text{V} \]

The DC component (5 V) is blocked by the transformer, so only the AC component is transformed.

Answer: B) 2400 V AC only

Question 2: Electric Motor Function

An electric motor transforms:

A) mechanical energy into electrical energy

B) electrical energy into mechanical energy

C) potential energy into electrical energy

D) a high voltage into a smaller voltage

E) a small voltage into a higher voltage

Solution – Explanation

An electric motor converts electrical energy into mechanical energy through the interaction of magnetic fields and current-carrying conductors. This is based on the motor effect, where a current-carrying conductor in a magnetic field experiences a force.

The reverse process (mechanical to electrical) is performed by electric generators.

Answer: B) electrical energy into mechanical energy

Question 3: Transformer Efficiency Calculation

A transformer with 80% efficiency is connected to a 50 V AC source. The secondary voltage and current are 500 V and 0.1 A respectively. What is the current in the primary?

A) 0.8 A

B) 1.0 A

C) 1.25 A

D) 1.35 A

E) 1.15 A

Solution – Explanation

Transformer efficiency (\(\eta\)) is defined as:

\[ \eta = \frac{\text{Output Power}}{\text{Input Power}} = \frac{P_{\text{out}}}{P_{\text{in}}} \]

For a transformer:

\[ \eta = \frac{V_s I_s}{V_p I_p} \]

Where:

\(\eta = 0.8\) (80% efficiency)
\(V_s = 500\ \text{V}\) (secondary voltage)
\(I_s = 0.1\ \text{A}\) (secondary current)
\(V_p = 50\ \text{V}\) (primary voltage)
\(I_p = ?\) (primary current, what we need to find)

Rearranging the formula to solve for \(I_p\):

\[ I_p = \frac{V_s I_s}{\eta V_p} = \frac{(500\ \text{V})(0.1\ \text{A})}{(0.8)(50\ \text{V})} \] \[ I_p = \frac{50\ \text{W}}{40\ \text{W/A}} = 1.25\ \text{A} \]

Note: For an ideal (100% efficient) transformer, \(V_p I_p = V_s I_s\). Real transformers have losses due to resistance, hysteresis, and eddy currents.

Answer: C) 1.25 A

Question 4: Motional EMF and Current

A bar of length \(L\) slides along electrical wires perpendicular to a magnetic field \(B\) directed out of the page. The bar and wires (including resistor \(R\)) form a closed circuit. Which action(s) will increase the current through \(R\)? (Assume negligible resistance in wires and bar.)

I. Decreasing the magnitude of \(B\)

II. Moving the bar faster

III. Increasing the length \(L\) of the bar

Diagram of a bar sliding on wires in a magnetic field

: Conducting bar moving in a magnetic field generates motional EMF

A) I only

B) II only

C) III only

D) II and/or III

E) I, II, and III

Solution – Explanation

The motional electromotive force (EMF) generated in the moving bar is given by:

\[ \mathcal{E} = B L v \]

Where:

\(B\) = magnetic field strength
\(L\) = length of the bar
\(v\) = velocity of the bar

The current in the circuit is given by Ohm's Law:

\[ I = \frac{\mathcal{E}}{R} = \frac{B L v}{R} \]

From this equation, we can see that:

Decreasing \(B\) would decrease the current (so I is incorrect)
Increasing \(v\) (moving faster) would increase the current
Increasing \(L\) would increase the current

Therefore, actions II and III would increase the current.

Answer: D) II and/or III

Question 5: Magnet Moving Through a Loop (Lenz's Law)

A permanent magnet is inserted at constant speed into a loop from the left and exits from the right as shown. While the magnet moves from left to right:

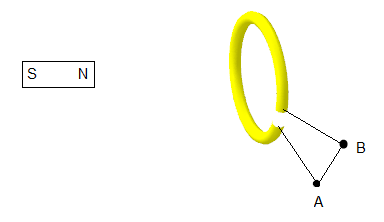
Diagram of a magnet moving through a loop

: Magnet moving through a conducting loop

A) the current in the loop will be from A to B

B) the current in the loop will be from A to B and then from B to A

C) the current in the loop will be from B to A

D) the current in the loop will be from B to A and then from A to B

E) there is no current in the loop

Solution – Explanation

Key Concept - Lenz's Law:

The direction of induced current is such that it opposes the change in magnetic flux that produced it. This is a consequence of the conservation of energy.

As the north pole of the magnet approaches the loop (from the left), the magnetic flux through the loop increases. According to Lenz's Law, the induced current will create a magnetic field that opposes this increase. Using the right-hand rule, this requires a current flowing from A to B.

When the magnet is exiting (south pole leaving the loop on the right side), the magnetic flux through the loop decreases. The induced current will now create a magnetic field that opposes this decrease, which requires the current to reverse direction (from B to A).

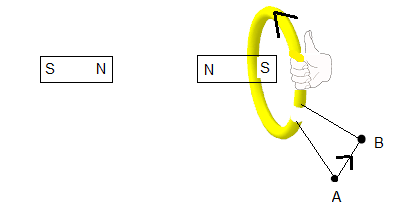
Solution diagram showing current direction as magnet approaches

: Current direction as magnet approaches the loop

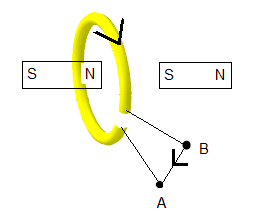
Solution diagram showing current direction as magnet leaves

: Current direction as magnet leaves the loop

Thus, the current changes direction during the process: A→B when the magnet enters, and B→A when it exits.

Answer: B) the current in the loop will be from A to B and then from B to A

Question 6: Induced Current Graph

A stationary magnet is pushed closer to a loop and then stopped. Which graph best represents the induced current in the loop?

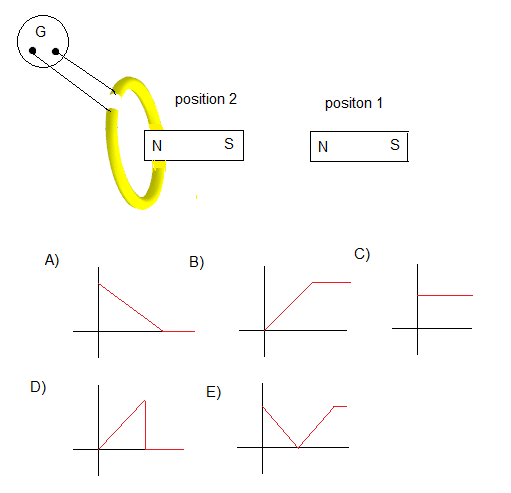
Multiple choice graphs of current vs. time

Figure: Possible current vs. time graphs

Solution – Explanation

According to Faraday's Law of electromagnetic induction:

\[ \mathcal{E} = -\frac{d\Phi_B}{dt} \]

Where \(\Phi_B\) is the magnetic flux. The induced current is proportional to the rate of change of magnetic flux.

Analyzing each phase:

Initially: Magnet is stationary, no change in flux → no induced current (\(I = 0\)).
While being pushed: Magnetic flux through the loop changes → current is induced.
When stopped: No change in flux → current returns to zero.

The correct graph must show zero current initially, then non-zero current while the magnet is moving, then zero again when it stops.

Answer: D (Graph showing current only while the magnet is moving)

Question 7: Magnetic Flux Calculation

A uniform magnetic field \(B\) is parallel to a rectangular surface with area 0.05 m² and field strength 0.5 T. What is the magnetic flux through the rectangle?

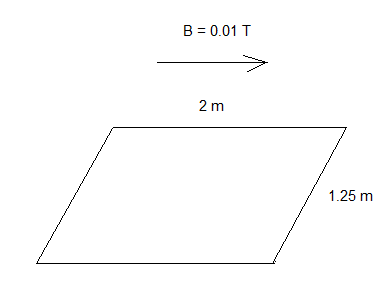
Diagram of magnetic field parallel to a rectangle

Figure: Magnetic field parallel to a rectangular surface

A) 0.025 Wb

B) 0 Wb

C) 0.004 Wb

D) 250 Wb

E) 0.01 Wb

Solution – Explanation

Magnetic flux (\(\Phi_B\)) through a surface is given by:

\[ \Phi_B = B A \cos\theta \]

Where:

\(B\) = magnetic field strength = 0.5 T
\(A\) = area of the surface = 0.05 m²
\(\theta\) = angle between magnetic field and normal to the surface

Since the magnetic field is parallel to the surface, it is perpendicular to the surface normal. Therefore, \(\theta = 90^\circ\) and \(\cos 90^\circ = 0\).

\[ \Phi_B = (0.5\ \text{T})(0.05\ \text{m}^2)(\cos 90^\circ) = (0.5)(0.05)(0) = 0\ \text{Wb} \]

Note: Magnetic flux is maximum when the field is perpendicular to the surface (\(\theta = 0^\circ\)) and zero when parallel to the surface (\(\theta = 90^\circ\)).

Answer: B) 0 Wb

Question 8: Non-Ideal Transformer Power Relationship

For a transformer that is not 100% efficient, which statement must be true?

A) \(V_p = V_s\)

B) \(V_s I_s > V_p I_p\)

C) \(V_s I_s = V_p I_p\)

D) \(I_p = I_s\)

E) \(V_s I_s < V_p I_p\)

Solution – Explanation

The efficiency (\(\eta\)) of a transformer is defined as:

\[ \eta = \frac{\text{Output Power}}{\text{Input Power}} = \frac{V_s I_s}{V_p I_p} \]

For a transformer that is not 100% efficient, \(\eta < 1\). Therefore:

\[ \frac{V_s I_s}{V_p I_p} < 1 \] \[ V_s I_s < V_p I_p \]

The input power exceeds the output power due to energy losses (resistive heating, hysteresis, eddy currents).

Answer: E) \(V_s I_s < V_p I_p\)

Question 9: Law for Direction of Induced Current

Which law determines the direction of induced current in a loop near a moving magnet?

A) Kirchhoff's law

B) Faraday's law

C) Joule's law

D) Lenz's law

E) Ohm's law

Solution – Explanation

Faraday's Law gives the magnitude of induced EMF: \(\mathcal{E} = -\frac{d\Phi_B}{dt}\)
Lenz's Law gives the direction of induced current: The induced current flows in a direction that opposes the change in magnetic flux that produced it.

While Faraday's Law tells us that an EMF will be induced when magnetic flux changes, Lenz's Law specifically determines the direction of the induced current.

Answer: D) Lenz's law

Question 10: Lenz's Law Principles

Which statements are true about Lenz's Law?

I. It obeys Newton's Third Law

II. It obeys the conservation of energy

III. It may be used to find the direction of induced current

A) I, II, and III

B) I and II only

C) I and III only

D) I only

E) II only

Solution – Explanation

Evaluating each statement:

I. It obeys Newton's Third Law: True. The force on the magnet due to the induced current is equal and opposite to the force causing the change in flux.

II. It obeys the conservation of energy: True. Lenz's Law ensures that the induced current opposes the change, meaning work must be done to cause the change. This work becomes the electrical energy in the induced current, conserving energy overall.

III. It may be used to find the direction of induced current: True. This is the primary application of Lenz's Law.

Answer: A) I, II, and III

Summary of Key Formulas:

Transformer equation: \(\frac{V_s}{V_p} = \frac{N_s}{N_p}\)
Transformer efficiency: \(\eta = \frac{V_s I_s}{V_p I_p}\)
Motional EMF: \(\mathcal{E} = B L v\)
Magnetic flux: \(\Phi_B = B A \cos\theta\)
Faraday's Law: \(\mathcal{E} = -\frac{d\Phi_B}{dt}\)
Lenz's Law: Induced current opposes the change in magnetic flux

SAT Physics Electromagnetism Practice Questions & Solutions

For more physics resources, visit ProblemsPhysics.com