
We present examples of circuits with series and parallel resistors and the formulas to calculate the equivalent resistance of these groups of resistors.
The resistors \( R_1, R_2, ..., R_m \) in the circuit on the left side are said to be in series because the same current passes through them. They behave in the same way as the circuit on the right of resistance \( R_{eq} \) given by the sum of the resistances:
\[ R_{eq} = R_1 + R_2 + ... + R_m \]

The voltage across each of the resistors \( R_1, R_2, ..., R_m \) in the circuit on the left is the same, and therefore these resistors are said to be in parallel. They behave in the same way as the circuit on the right of resistance \( R_{eq} \) given by:
\[ \frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} + ... + \frac{1}{R_m} \]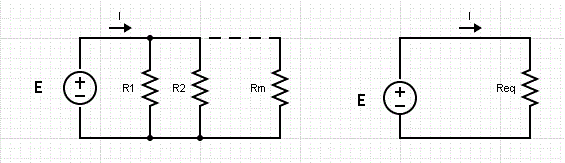
Find the current \( I \) passing through and the voltage across each of the resistors in the circuit below.
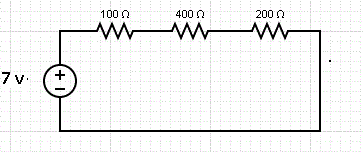

Multiplying by 400: \[ \frac{400}{R_{eq}} = 4 + 1 + 2 \] Solving for \( R_{eq} \): \[ R_{eq} = \frac{400}{7} \Omega \] The main current \( I \) is given by: \[ I = \frac{7}{R_{eq}} = \frac{7}{(400/7)} = \frac{49}{400} A \] We now use Ohm's law to find the current passing through each resistor.
The current through the resistor of \( 100 \,\Omega \): \[ I_1 = \frac{7}{100} \text{ A} \] The current through the resistor of \( 400 \,\Omega \): \[ I_2 = \frac{7}{400} \text{ A} \] The current through the resistor of \( 200 \,\Omega \): \[ I_3 = \frac{7}{200} \text{ A} \] As an exercise, check that the sum of the three currents above is equal to the total current: \[ I = \frac{49}{400} \text{ A} \]
Find current \( I \) in the circuit below.

\[ \frac{1}{50} = \frac{1}{100} + \frac{1}{200} + \frac{1}{x} \] Solving for \( x \): \[ \frac{1}{x} = \frac{1}{50} - \frac{1}{100} - \frac{1}{200} \] \[ \frac{1}{x} = \frac{4}{200} - \frac{2}{200} - \frac{1}{200} = \frac{1}{200} \] \[ x = 200 \Omega \]
Show that if the resistors with resistances \( R_1, R_2, \dots, R_m \) are in parallel, then the equivalent resistance \( R_{\text{eq}} \) is always smaller than \( R_1, R_2, \dots, R_m \).
The equivalent resistance \( R_{\text{eq}} \) is given by the equation:
\[
\frac{1}{R_{\text{eq}}} = \frac{1}{R_1} + \frac{1}{R_2} + \dots + \frac{1}{R_m}
\]
Since \( R_{eq}, R_1, R_2, \dots, R_m \) are positive quantities, we can write:
\[
\frac{1}{R_{\text{eq}}} > \frac{1}{R_i}
\]
where \( R_i \) is any of the resistances \( R_1, R_2, \dots, R_m \).
Multiplying all terms of the inequality above by \( R_{\text{eq}} \times R_i \) and simplifying, we obtain:
\[
R_i > R_{\text{eq}}
\]
or equivalently,
\[
R_{\text{eq}} \lt R_i \; , \quad i = 1, 2, \dots, m.
\]